Equal Chords and their Distances from the Centre
Equal Chords and their Distances from the Centre: Overview
This topic covers concepts, such as, Equal Chords and their Distances from the Centre & Properties Related to Chord of a Circle etc.
Important Questions on Equal Chords and their Distances from the Centre
In a circle with radius , two equal chords are at a distance of from the centre. If the lengths of the chords is , then find the value of .
Find the ratio between the chords which are equidistant from the centre of a circle.
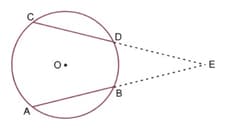
In given figure, AB and CD are equal chords of a circle with centre O. If AB and CD meet at E (outside the circle), prove that BE = DE.
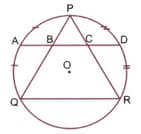
is an equilateral triangle inscribed in a circle. and are mid points of arcs and respectively. Prove that .
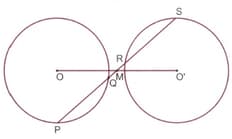
A straight line is drawn cutting two circles of equal radii and passing through the mid point M of the line joining their centres O and O'. Prove that the chords PQ and RS, which are intercepted by the two circles, are equal.
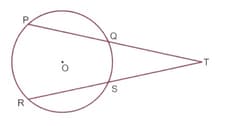
PQ and RS are two equal chords of a circle with centre O. If PQ and RS, on being produced meet at T outside the circle, prove that TQ = TS
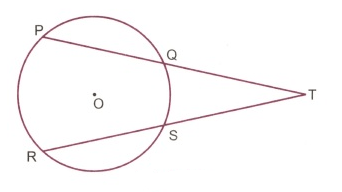
PQ and RS are two equal chords of a circle with centre O. If PQ and RS, on being produced meet at T outside the circle, prove that PT = RT
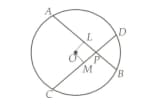
Two equal chords and of a circle intersect at a point within a circle then
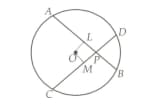
Two equal chords and of a circle intersect at a point within a circle then
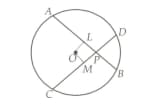
Two equal chords and of a circle intersect at a point within a circle then
Three chords and of a circle are respectively and away from the center. Which of the following is correct?
Which of the following statements is true for the longest chord of a circle?
Prove that, of any two chords of a circle, the greater chord is nearer to the centre.
Circles with centres and intersect at points and as shown in the figure. is a line segment and is tangent to the circle, with centre at point If the circles are congruent, show that
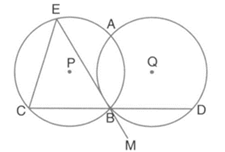
Two congruent circles of centres and intersects each other at point and , then prove that .
If two chords and are away from the centre of a circle, then .
The chords of a circle of length and . Which apart from the centre are and respectively.
Chords of a circle and are and , which makes angle at centre are of and respectively.
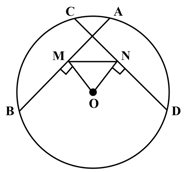
In the figure below, and are two equal chords of a circle and is the center of circle. If and , then prove that .
Prove that out of all chords which passes through any point of circle, that chord will be smallest which is perpendicular on diameter which passes through that point .
